Bloom Filter

Bloom Filter 소개

실제 존재하는지는 확실하지 않지만, 부재 하다는 것은 확실하게 알 수 있음

Cassandra의 SSTable (LSM Tree), 50개의 SSTable과 corresponding bloom filter가 있음. 첫 bloom filter lookup에서 not present이면 다음 bloom filter로 라우팅. 만약 present라고 뜨면 disk를 읽어서 실재하는지 확인, 없으면 또 다음 bloom filter로 라우팅

공간 (m), 항목 수(n), 해시 함수(k), false positive rate (f)

Quotient Filter

Bloom Filter처럼 False positive를 대가로 공간도 절약하지만, 다른 이점도 있음 ㄱㄷ

3.1 Bloom Filter 작동 방식

모든 슬롯은 초기에 0 으로 설정되어있는 bit array이다. $A[0..m-1]$ $k$ 개의 독립적인 해시 함수 $h_1, h_2, …, h_k$ 이고, 해시함수의 결과는 $[0,m-1]$ 범위에 uniform random하게 매핑됨

3.1.1 Insert

element $x$ 를 넣는다면, 모든 해시 함수의 결과를 계산해서 어레이에 저장

hashes: List[Callable[[Any], int]]
k: int = len(filter_functions)

def insert(e) -> None:
    for i in range(k):
        A[hashes[i](e)] = 1

insert(x)를 할때 $h_1(x) = 1, h_2(x) = 5$ 라면, 배열의 1,5번째 index에 1을 저장

insert(y)를 할때 $h_1(y) = 4, h_2(y) = 6$ 이라면, 배열의 2, 6 번째 index에 1을 저장.

따라서 배열의 값은 0 1 0 0 1 1 1 0 이 된다.

시간복잡도: O(k), 대체적으로 12개 이하

3.1.2 Lookup

def lookup(e) -> bool:
    for i in range(k):
        if A[hashes[i](x)] == 0:
            return False # not present
    return True # present

lookup(x) 를 한다면 $h_1, h_2$ 의 결과는 각각 1, 5 이고 둘다 배열에 1이 들어있으므로 true 리턴.

lookup(z) 를 할때 $h_1, h_2$ 의 결과가 각각 4, 5 가 나온다면 둘다 배열에 1이 들어있어서 true를 리턴, 하지만 실제 값은 없으므로 false positive임

시간복잡도: worst O(k)인데, 존재하지않으면 대체적으로 k회만큼 조회하진 않음.

사용 사례

3.2.1 Squid: web proxy cache

web proxy는 cache를 이용해서 data copy를 유지해서 웹 트래픽을 줄임. 각각의 proxy가 이웃 proxy의 cache를 저장하거나, bloom filter를 활용해서 이웃 proxy에 데이터가 존재하는지도 저장해둠.

유저의 요청이 web proxy A 에 도착하면.

1. A는 자신의 cache에 데이터가 존재하는지 확인
2. cache에 데이터가 없으면, Bloom Filter를 통해서 인접한 proxy B, C, D에 해당 요청에 대한 데이터가 존재하는지 확인
3. Bloom Filter에서 proxy D에 데이터가 존재하는것으로 확인되면 D에 요청을 forward함 다만 데이터는 stale해질수도 있으므로 (D에 실제 존재했지만 D에서 데이터를 제거하는경우) false positive는 더 발생할 수 있음.

3.4 Bloom Filter 구성

• $n$: 넣을 element 수
• $f$: false positive rate
• $m$: bloom filter의 비트 수

• $k$: hash function 수

• 식 3.1 - false positive rate을 결정하는 공식

$f \approx (1 - e^{-(nk/m)})^k$

위 식을 시각적으로 이해해보자

$m/n$ (element 수 당 bit의 비율), $k$ (hash function 수)에 따른 false positive rate을 보여주는 그래프.

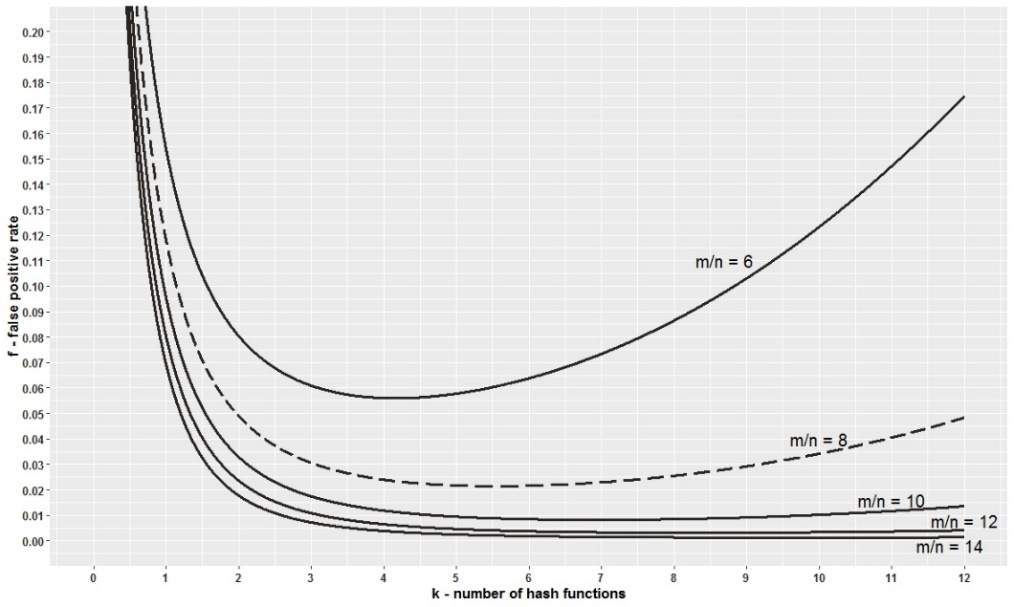
실제 application에선 $m/n$을 일정하게 가져간다. 대체적으로 [6, 14]의 범위면 false positive rate이 낮아진다.

$m/n$ 을 크게 키울수록 공간이 많아지므로 false positive rate이 내려감.

$m/n$ 을 고정했을때 $k$를 증가시킨다고해서 무조건 false positive rate이 무조건 낮아지는건 아님 (hash value 경우의 수가 늘어나므로)

최적의 $k$ 값은 위의 false positive 공식을 미분하면 알아낼 수 있음

• 식 3.2 - 최적의 $k$ 결정 $k_{opt} = m/n*ln2$

$m/n = 8$ 일때 $k_{opt} = 5.545$

$k_{opt}$를 사용하면 false positive rate이 같아진다

• 식 3.3 - 최적의 $f$ 결정

$f_{opt} = (1/2)^k$.

$k_{opt}$ 식을 FPR 공식에 대입하면 나온다.

bloom filter를 생성할땐 $n$, $f$를 입력받아서 $m$, $k$를 생성하는데, $k_{opt}$ 가 정수가 아닐경우 반올림을 하게되니 정확한 $f_{opt}$가 달라진다. 하지만 $f_{opt}$ 공식을 활용해서 생기는 오차는 크지 않으며, 반올림보다는 계산하는 hash function의 수를 불이기 위해 값을 내리는게 낫다. (즉 5.545에서 5 선택)

또한 $f_{opt}$를 보면 동전던지기와 비슷한데 k개의 연속된 1이 발생하면 false positive가 발생한다. 따라서 bloom filter에 0/1 skew가 크게 있으면 잘 동작하지 않을 것이다.

Bloom filter에서 주어진 parameter가 있을때 남은 parameter를 구하는 예시

예제 1) m, n, k 에서 f 계산: 처음에 1M개의 element를 저장하도록 만들었지만, element수를 10배로 늘릴경우 기존 bloom filter의 FPR을 구해보자. m=3MB=3810^6, n=1M -> 10M=10^7, k=2 이다.

$f = (1-e^{-nk/m})^k = (1 - e^{-210^7/(38*10^6)})^2 = (1-(1/e)^{5/6})^2 = 32%$

예제 2) n, m 에서 f, k 계산: 1M개의 element를 저장하는 bloom filter 만들기.

• $m=1MB=8*10^6$
• $k_{opt} = m/nln2 = 810^6/10^6*ln2 = 5.54$

3.5 단점

단점

• 삭제 불가능
• 크기 조정이 어려움
• input 자체가 random하지 않으면 문제가 생김
  • 현실은 대부분 zipfian distribution 이므로 frequent element에서 FPR이 올라가면 전체적으로 FPR이 올라감.