Ref) Algorithms and Data Structures for Massive Datasets

• HyperLogLog
  • 1. count distinct의 동작
  • 2 HyperLogLog를 보기전 천천히 이해해보자
    • 2.1 직관
  • 3 확률론적 평균화
  • 4 LogLog
    • 4.1 LogLog의 필요 저장공간, 왜 이름이 LogLog?
  • 5 HyperLogLog
  • 6 Trino 지원 함수

HyperLogLog

1. count distinct의 동작

SELECT COUNT(DISTINCT col) FROM table

정렬되어있지 않은경우, 정렬이 필요함. 정렬 후 데이터를 순차적으로 읽어 중복을 제거할 수 있음.

이 문제를 Element distinctness problem 이라 하는데, 정렬이 아닌 다른 방식으로도 해결될 수 있지만 시간 복잡도는 $\Theta(nlogn)$ 이라고 함.

해시테이블을 쓰려고 해도 distinct element 수 $k$ 는 실제 element 수 $n$까지 증가할 수 있으므로 해싱을 사용하기 부적합함

2 HyperLogLog를 보기전 천천히 이해해보자

• $a_1, a_2, …, a_n$: 원본 데이터 (이중 distinct element $k$개)
• $h_1, h_2, …, h_n$: $a_i$의 해시값

$\rho_i$: (위 $h_i$ 에서 연속적으로 0으로 끝나는 0의 개수) + 1

• $h_1$ = 1111 이면, $\rho_1$ = 1
• $h_2$ = 1000 이면, $\rho_2$ = 4

$\rho_{max} = max(\rho_1, \rho_2, … \rho_n)$

카디널리티 추정값 $E$ = $2^{\rho_{max}}$

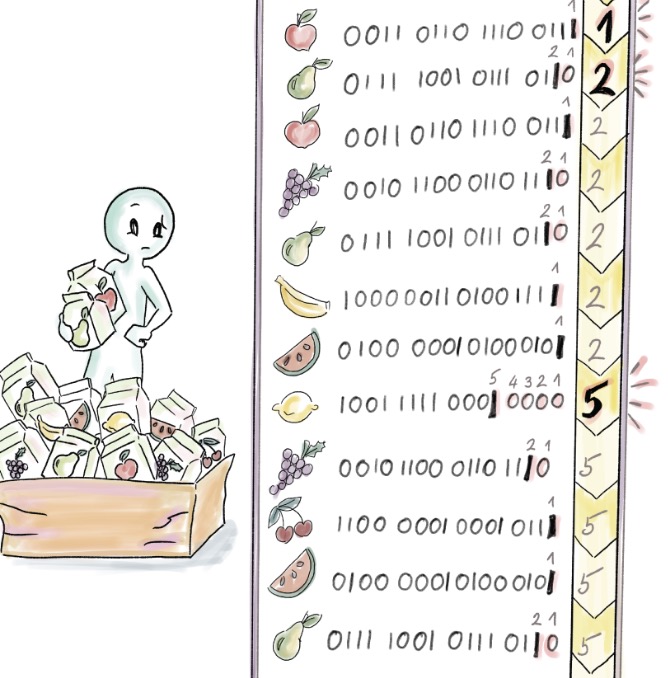
• 이 예시에서 element 수 는 12, distinct element 수는 7
• $\rho_{max} = 5$, $E = 2^5 = 32$
• 실제 값 7과의 격차는 아직 크다

2.1 직관

• k개의 bit array가 uniform random 할때
• 마지막 bit가 0으로 끝날 확률은 $k/2$, 1로 끝날 확률도 $k/2$, 그리고 00, 01, 10, 11로 끝날 확률은 $k/{2^2}$

따라서

• $\rho_i = 1$ (해시값이 1로 끝나는 경우) 인 해시를 생성할 확률은 $1/2$
• $\rho_i = 2$ (해시값이 10으로 끝나는 경우)일 확률은 $1/4$
• $\rho_i = j$ (해시값의 $10^{j-1}$로 끝나는경우)일 확률은 $1/2^{j}$
• => $1/2^j$ 의 확률이 발생하려면 평균적으로 $2^j$ 의 반복이 필요하므로, $\rho_{max}$가 생겼다는것은 $2^{\rho_{max}}$의 카디널리티가 존재한다고 생각할 수 있음
• 10% 주문서를 성공하려면 10개 주문서를 사두면 성공할것이라는 기대를 가지는것과 같은 맥락

어찌됐건 확률의 평균적인 행동을 가지고 기대값을 만든것이므로 실제와 다를 수 있음.

3 확률론적 평균화

“2 HyperLogLog를 보기전 천천히 이해해보자” 에서 기대값 $E = 2^{\rho_{max}}$ 인데, 이게 2의 지수이므로 실제 카디널리티와 가까워지기 힘듦

따라서 여러 버킷으로 쪼개어서 각 버킷에 대해 확률적 계산을 수행해보자.

• 각 해시값 $h_i$ 에서 처음 $b$개의 bit를 가지고 버킷을 선택 ($m=2^b$ 개의 버킷이 존재)
• 그리고 “2 HyperLogLog를 보기전 천천히 이해해보자” 의 $\rho_i$ 를 계산, 그러면 $m$개의 bucket에서 $\rho_{max}$ 값 $m$개가 생김 -> $\rho_{i,max}$
• 위 $m$개의 b버킷에서 산술평균을 계산하면, $A = \frac{\Sigma_{i=1}^{m}\rho_{i,max}}{m}$
• 그리고 산술평균으로 “평균 버킷 추정”, $E_{bucket} = 2^{A}$
• “평균” 버킷 추정이므로 전체로 확장하면, $E = m * E_{bucket} = 2^{\frac{\Sigma_{i=1}^{m}\rho_{i,max}}{m}}$

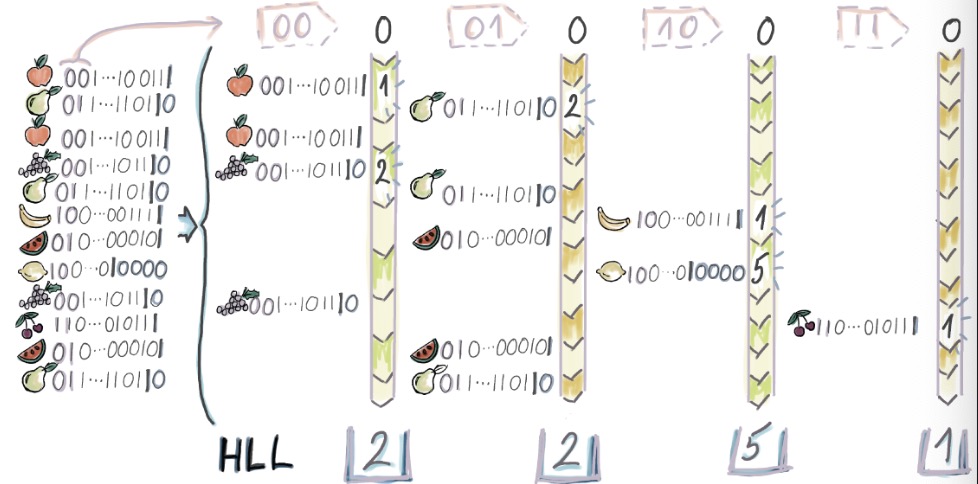
• 위 예시에서 $b=2, m=4$
• 각 4개 버킷의 $\rho_{i, max}$ 는 각각 $2, 2, 5, 1$
• $A = \frac{2+2+5+1}{4} = 2.5$
• $E_{bucket} = 2^{A} = 2^{2.5} \approx 5.66 $
• $E = m * E_{bucket} = 4 * 5.66 = 22.64$
• “2 HyperLogLog를 보기전 천천히 이해해보자” 에서는 32, 실제 카디널리티는 7. 아직 값이 부정확하지만 이전보다 정확해졌음

4 LogLog

LogLog 는 1.3의 확률론적 평균화에서 정규화상수 $~a_m$ 을 사용함

$~a_m$ 은 버킷 수 m에서부터 생성되는 상수, $~a_m \sim 0.39701 - \frac{2\pi^2+(ln2)^2}{48m}$

• 통상적으로 $m >= 64$ 일때 $~a_m = 0.39701$을 사용함

그리고 확률론적 평균화의 카디널리티 추정값 $E = m * E_{bucket}$ 에서 $~a_m$ 을 곱한 값을 카디널리티 추정값으로 사용

$E = ~a_m * m * E_{bucket}$

• “3 확률론적 평균화” 의 예시에서 m=4이므로, $~a_m = ~a_4 = 0.39701 - \frac{2\pi^2+(ln2)^2}{48*4} = 0.292$
• $E = ~a_m * m * E_{bucket} = 0.292 * 4 * 5.66 \approx 6.6$
• 실제 값과 매우 가까워지게 됨

4.1 LogLog의 필요 저장공간, 왜 이름이 LogLog?

LogLog의 relative error는 $1.3/\sqrt{m}$ 에 가깝다고 함.

$m=2^{14}$ 로 설정한다면 (해시값에서 앞 14개의 bit사용, 2^14=16384 개 버킷), “데이터 셋의 크기”에 관계없이 $1.3/\sqrt{2^{14}} = 1.01%$ 의 relative error를 기대할 수 있음

• 한 버킷에서 버킷카운터 값 한개 $\rho_{i,max}$ 만 유지하면 되므로, 이걸 8byte인 long 으로 설정한다면 $2^3*2^{14} = 131072$ = 130KB 만 필요함

실제 버킷 카운터의 비트 수를 계산해보자..

1. 카디널리티의 최대값이 $k_{max}$ 이면
   • 예시) 30일 MAU를 구한다고 했을때 이 값의 상한은 그동안 가입한 모든 유저 수가 될것
   • $k_{max}$ 를 5천만이라고 해보자 10 1111 1010 1111 0000 1000 0000
2. 해당 카디널리티까지 구분하기 위한 해시 길이는 $O(log_2k_{max})$ 여야 함
   • 카디널리티의 최대값에 $log_2$를 씌우면 최대값이 가진 비트 개수가 됨
   • 5천만개 경우의수 전부를 해시를 한다면 해시의 최대 범위는 5천만이면 된다. 즉 5천만을 담을 수 있는 비트만 필요함
   • $log_250000000 = 25.575$, 26개의 bit
3. 그리고 버킷의 최대 값 저장을 위해선 $O(mlog_2{log_2k_{max}})$ 개의 비트가 필요하다
   • 버킷 카운터 값 $\rho$ 는 연속된 0의 개수 + 1이므로 $log_2k_{max}$ = 26 이라는 값을 담을 수 있는 bit면 됨
   • 즉 버킷 카운터 공간은 5bit 만큼만 있으면 됨
   • 그리고 버킷이 $m$개가 있으므로 $5 bit * 2^{14} = 81920$ 약 81KB
   • $k_{max}$를 long max인 2^64로 한다고 해도 $2^{14}*log_2{log_2{2^{64}}}=98304$, 98KB

5 HyperLogLog

“4 LogLog” 에서 버킷의 산술평균 대신 조화평균을 사용해보자

$E_{bucket}=\frac{m}{\Sigma_{i=1}{m}2^{-\rho{i,max}}}$

최종 카디널리티 계산은

$E = \alpha_m * m * E_{bucket} =$ $\frac{\alpha_m m^2}{\Sigma_{i=1}{m}2^{-\rho_{i,max}}}$

편항 보정계수는 LogLog와는 다른 값을 사용함

$\alpha_m=\frac{1}{2ln2(1+\frac{1}{m}(3ln2-1)+O(m^{-2}))}$

“3 확률론적 평균화” 의 예시에 조화평균 적용 $E_{bucket}=\frac{4}{(1/2)^2 + (1/2)^2 + (1/2)^5 + (1/2)^1} = \frac{4}{33/32} \approx 3.88$

$\alpha_4=0.541$ 이므로 $E = 0.541 * 4 * 3.88 = 8.39$

• LogLog 에선 6.6이 나왔고, HyperLogLog에서는 8.39가 나와서 정답 7 보다는 더 멀어졌지만, 데이터셋이 커질수록 HyperLogLog의 편향과 상대오차가 적다고 함
• HyperLogLog의 상대오차는 $\frac{1.04}{\sqrt{m}}$ 이하이므로, LogLog의 상대오차 $\frac{1.3}{\sqrt{m}}$ 보다 작음

6 Trino 지원 함수

HyperLogLog에서 계산한 데이터들 자체를 저장해두고, 버킷 크기 $m$이 같은 HyperLogLog 두개를 합칠 수 있음

https://trino.io/docs/current/functions/hyperloglog.html

approx_set(x) → HyperLogLog Returns the HyperLogLog sketch of the input data set of x. This data sketch underlies approx_distinct() and can be stored and used later by calling cardinality().

cardinality(hll) → bigint This will perform approx_distinct() on the data summarized by the hll HyperLogLog data sketch.

empty_approx_set() → HyperLogLog Returns an empty HyperLogLog.

merge(HyperLogLog) → HyperLogLog Returns the HyperLogLog of the aggregate union of the individual hll HyperLogLog structures.

예시) 매일 최근 30일 MAU 구하기

• count distinct를 사용하게 되면 -> 매일 30일 범위의 데이터를 스캔해야함
  • 30일동안 매일 MAU를 계산한다면 30*30 = 900일치 데이터에 대한 연산이 생기는것
• HLL을 사용하면, 매일 1일 범위의 HLL 데이터를 생성하고, 30일 범위의 HLL 데이터를 스캔해서 merge 후 카디널리티 계산
  • 30일동안 매일 MAU를 계산한다면 30 + 29(첫날 기준 이전29일 데이터에 대해 HLL 미리 생성 필요)일의 HLL 생성과, 저장된 HLL 데이터를 merge하기 위해서 추가적인 스캔(매우작음) 필요.

데이터 생성할때

INSERT INTO sketch AS
SELECT
    "2024-05-01" AS date,
    CAST(
        approx_set(user_id) -- HLL sketch 생성
    AS VARBINARY) AS hll -- 저장할땐 VARBINARY type으로 저장
FROM logs
WHERE time >= "2024-05-01" AND time < "2024-05-02"

계산할때

SELECT
    CARDINALITY(
        MERGE(
            CAST(hll AS HyperLogLog) -- VARBINARY 에서 HyperLogLog로 캐스팅
        ) -- HLL structure들을 병합
    ) AS approx_distinct_count -- 병합된 HLL에서 카디널리티 계산
FROM sketch
WHERE date >= "2024-05-01" AND date < "2024-06-01"